A prova original, assim como seu gabarito, se encontram em:
Vestibular Uerj 2008
Enunciado
33) Duas partículas, X e Y, em movimento retilíneo uniforme, têm velocidades respectivamente iguais a 0,2 km/s e 0,1 km/s.
Em um certo instante t1 , X está na posição A e Y na posição B, sendo a distância entre ambas de 10 km.
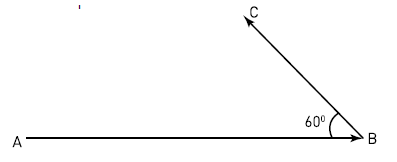
As direções e os sentidos dos movimentos das partículas são indicados pelos segmentos orientados AB e BC, e o ângulo ABC mede 600, conforme o esquema.
Sabendo-se que a distância mínima entre X e Y vai ocorrer em um instante t2, o valor inteiro mais próximo de t2 - t1 , em segundos, equivale a:
(A) 24
(B) 36
(C) 50
(D) 72
Resolução
É razoável imaginar que a menor distância entre os dois móveis ocorrerá quando ambos estiverem próximos de uma mesmo vertical, como na figura abaixo:
Lembrando que a distância entre dois pontos A (xA,yA) e B(xB,yB) é dada por:
d(A,B) = [(Xa - Xb)² + (Ya - Yb)²]1/2 = [(Xa - Xb)² + (0 - Yb)²]1/2
Esse valor será mínimo quando Xa = Xb, isto é, quando as partículas estiverem sobre uma mesma vertical!
Considerando a componente horizontal da partícula Y, as duas estarão na mesma vertical quando X = Yhorizontal, onde:
X = 0 + 0,2.t (tomando o ponto A como origem dos espaços horizontais)
Yhorizontal = 10 - 0,1.cos (60).t [-0,1.cos (60) é a compontente horizontal da velocidade de Y!]
Para X = Yhorizontal teremos:
0,2.t = 10 - 0,1.0,5.t
0,25.t = 10
t = 10/0,25 = 40 => O inteiro mais próximo deste valor é 36!
Resposta (B)
Comentário
Questão interdisciplinar difícil. O candidato precisa saber calcular a distância entre dois pontos, trabalhar com a componente horizontal do movimento que segue a semi-reta BC e conectar tudo isso com o problema do encontro de dois móveis!
Os conceitos de física (Movimento Uniforme e Componente de um vetor) são simples, mas a análise do problema pode não ser trivial para a maior parte dos candidatos!