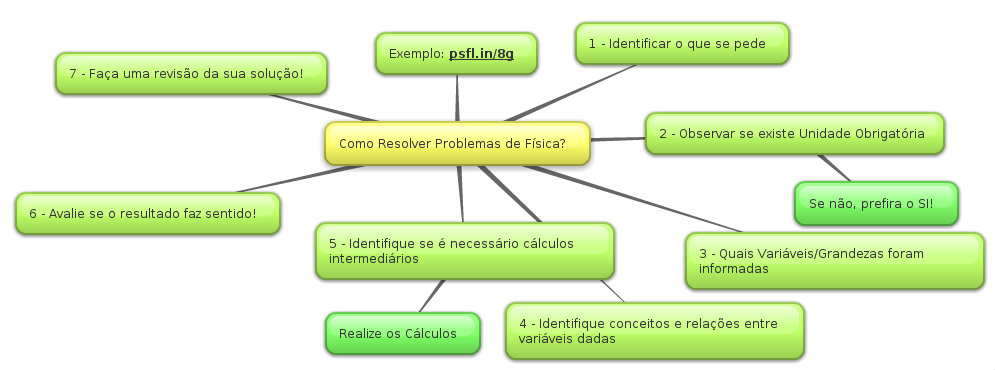
Posted by admin on 19 Mar 2012 in cinemática, Mapas Mentais
Category: "cinemática"
- 1
- 2
Posted by admin on 15 Mar 2012 in cinemática, Termofísica
Definição
Em sistemas em equilíbrio térmico a grandeza física (escalar) que mede o grau de agitação média molecular (das partículas do sistema) é chamada de temperatura. A rigor, temperatura é a grandeza física que mede a energia cinética média de cada grau de liberdade de cada uma das partículas de um sistema.
Embora o conceito de Temperatura esteja relacionado com o de Calor, Temperatura NÃO É uma medida de energia do sistema, muito menos uma medida de Calor!
Mais sobre Temperatura? Comece na Wikipedia
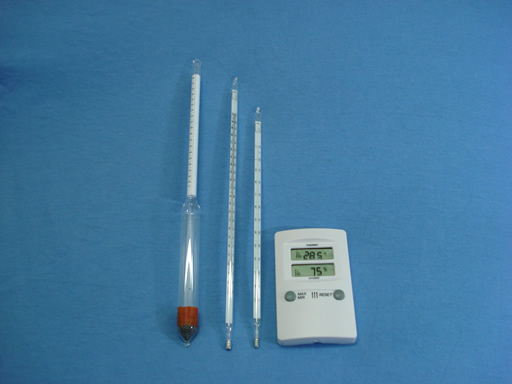
Medida de Temperatura
A medição da temperatura de um sistema é sempre feita de maneira indireta. Resumidamente coloca-se o sistema que se deseja medir a temperatura em equilíbrio térmico com o dispositivo que irá medir a temperatura (termômetro). Este dispositivo tem uma grandeza física que varia com a temperatura (grandeza termométrica).
Uma escala numérica (escala termométrica) associa então as mudanças na grandeza termométrica com a temperatura!
Assim existem vários tipos de termômetro, cada qual com uma grandeza termométrica diferente.
Escalas Termométricas
Uma escala numérica onde cada valor está associado a uma única temperatura. Na construção de escalas termométricas define-se valores numéricos arbitrários para duas temperaturas fixas (pontos fixos) e dividi-se o intervalo entre esses dois pontos fixos num certo número de partes.
As Escalas Termométricas mais utilizadas são a Celsius, a Fahrenheit e a Kelvin (SI).
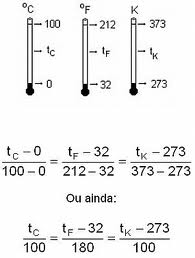
A relação entre a variação de temperatura nestas três escalas é dada por:
Como se pode observar a transformação de escalas termométricas é um simples problema de matemática (uma função entre duas ou mais escalas).
Posted by admin on 17 Jun 2011 in cinemática
Introdução
Como já sabemos, as grandezas cinemáticas, exceto o tempo, são grandezas vetoriais. Com isso, toda composição de movimentos pode ser pensada como a soma vetorial de algumas dessas grandezas (posição, velocidade ou aceleração).Composição de Dois Movimentos Uniformes
Se um móvel move-se com velocidadeComposição de um MU com um MUV
Quando um móvel se move próximo da superfície da Terra e sem resistência do ar, ele está sujeito apenas a aceleração da gravidade, que como sabemos, é constante, vertical e sempre apontada para baixo. Desse modo o movimento pode ser entendido como a composição de um movimento uniforme na horizontal com um movimento uniformemente variado na vertical: Veja a imagem abaixo para visualizar o que foi dito: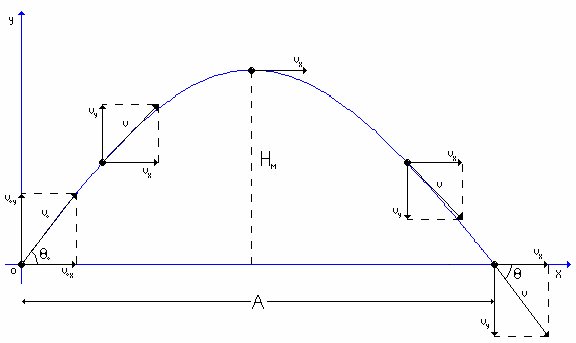
Logo os lançamento oblíquos podem ser resolvidos como dois movimentos simultâneos. As equações podem ser tratadas isoladamente tendo apenas em comum o tempo (pois são simultâneos). As velocidades iniciais de cada movimento são dadas por: Componente Horizontal:
Exemplos
Como exemplo do que foi dito vamos calcular, para um lançamento oblíquo, a partir do solo com velocidade V0 fazendo um ângulo (teta) com a horizontal qual será o tempo de voo, o alcance vertical máximo e o alcance horizontal do móvel: Tempo de Voo O tempo de voo é igual ao tempo de subida mais o tempo de descida. Como o tempo de subida é igual ao tempo de descida (mesmo módulo da aceleração e mesma distância) teremos que o tempo de voo é o dobro do tempo de subida: t(voo) = 2.t(subida) No ponto mais alto da trajetória a componente vertical da velocidade será zero, então usando a equação da velocidade para o MUV teremos: 0 = Voy - g.ts => ts = voy/g Logo: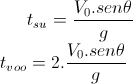 Alcance Vertical Máximo:Podemos calcular o alcance vertical máximo, por exemplo, aplicando a equação de torricelli ao movimento vertical. Como sabemos, no ponto mais alto da trajetória, a componente vertical da velocidade é nula:
0² - voy² - 2.g.h => h = voy²/2.g
Logo:
Alcance Vertical Máximo:Podemos calcular o alcance vertical máximo, por exemplo, aplicando a equação de torricelli ao movimento vertical. Como sabemos, no ponto mais alto da trajetória, a componente vertical da velocidade é nula:
0² - voy² - 2.g.h => h = voy²/2.g
Logo:
Applet
Uma simulação de lançamento de projéteis, para você explorar, estudar e aprender pode ser vista apontando seu navegador para este endereço (clique para ir para a página do Applet). Posted by admin on 17 Jun 2011 in cinemática
Introdução
Definição: Movimento em que a aceleração permanece constante. Isto é, a velocidade varia de modo uniforme. Assim temos dois casos:- Se somente o módulo do vetor velocidade varia temos um Movimento Retilíneo Uniformemente Variado (MRUV), pois a direção da velocidade não muda.
- Se o módulo do vetor velocidade varia temos um Movimento Uniformemente Variado (MUV), pois a direção da velocidade também pode mudar.
Eq. Horária da Posição
A Equação que relaciona a posição do móvel com o tempo, chama-se Equação Horária da Posição para o Movimento Uniformemente variado: S = So + Vo.t + a.t²/2 Onde: S = Posição ou Espaço final do Móvel; So = Posição ou Espaço inicial do Móvel; Vo = Velocidade Inicial do Móvel; a = Aceleração do Móvel; t = Instante de tempo.Eq. Horária da Velocidade
A Equação que relaciona a velocidade do móvel com o tempo, chama-se Equação Horária da Velocidade para o Movimento Uniformemente variado: V = Vo + a.t Onde: V = Velocidade final do Móvel; Vo = Velocidade Inicial do Móvel; a = Aceleração do Móvel; t = Instante de tempo.Gráficos do Movimento Uniformemente Variado
O gráfico da posição versus tempo será uma parábola (com concavidade para cima ou para baixo) pois é uma relação quadrática (do 2 grau):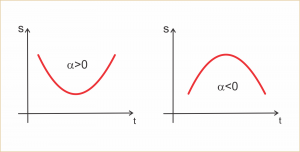
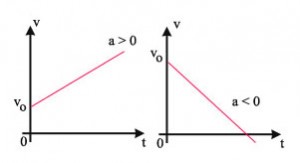
Posição versus Tempo O gráfico da velocidade versus tempo será uma reta (crescente ou decrescente) pois temos uma relação linear entre velocidade e tempo:
 O gráfico da aceleração versus tempo será uma reta paralela a eixo dos tempos:
O gráfico da aceleração versus tempo será uma reta paralela a eixo dos tempos:
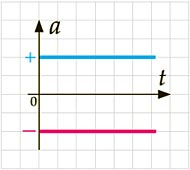
Gráfico da Aceleração Versus Tempo
Eq. Torricelli
Nos problemas de MUV onde o tempo não aparece nem nos dados nem na pergunta deveríamos usar as duas equações horárias do MUV simultanemanete. Uma alternativa seria juntar as duas equações numa única equação. Esta equação, deduzida da junção das duas equações horárias do MUV, chama-se: Equação de Torricelli. E não é uma equação horária: V² = Vo² + 2.a.(S-So) Onde: V = Velocidade Final do Móvel; Vo = Velocidade Inicial do Móvel; a = Aceleração do Móvel; S = Posição ou Espaço final do Móvel; So = Posição ou Espaço inicial do Móvel. Posted by admin on 17 Jun 2011 in cinemática
Introdução
Definição: Movimento em que a velocidade permanece constante (aceleração é igual a zero!). Assim temos dois casos:- Se o vetor velocidade é constante temos um Movimento Retilíneo Uniforme (MRU) (pois módulo, direção e sentido) da velocidade nunca mudam.
- Se o módulo da velocidade (ou a velocidade escalar) é constante temos um Movimento Uniforme.
Gráficos do Movimento Uniforme
O gráfico da posição versus tempo será uma reta (crescente ou decrescente) pois é uma relação linear: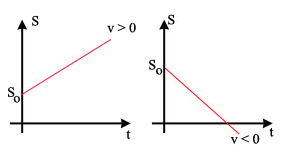
Gráfico Posição versus tempo - MU O gráfico da velocidade versus tempo será uma reta paralela ao eixo dos tempos:
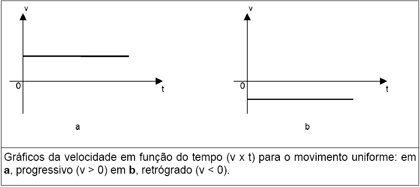
Gráfico velocidade versus tempo - MU
- 1
- 2